3.3.4. Sequential Representation

Sequential encoding modality presents a distinct approach from spatial encoding in its treatment of glyph data. Whilst spatial encoding considers the relative positioning of points in two-dimensional space, sequential encoding processes points as ordered instructions – rather like the difference between learning dance by observation versus following written choreography.

In sequential encoding, glyph data is interpreted as a series of ordered commands, whether as polylines, coordinate points, SVG directives, or Bézier path specifications. This methodology mirrors the inherent structure of vector graphics, which are fundamentally stored as notational sequences. The approach shares significant commonality with natural language processing techniques, where textual data is similarly encoded as sequential patterns.

The technical implementation involves transforming Bézier path data into numerical sequences suitable for machine learning applications. This transformation process can be demonstrated through two standard font file formats: .glyphs and .otf.

In both cases, the vector path data – comprising coordinates and control points – is converted into ordered sequences of numerical values.

The encoding process necessitates data normalisation to facilitate machine learning computations. This normalisation transforms the raw coordinate values into a consistent range of 0.0-1.0, which enables the neural network to compute weights effectively. The process involves dividing coordinate values by the em-square size – typically 1000 units per em (UPM) for PostScript-based OpenType fonts or 2048 UPM for TrueType-based fonts. Whilst the valid range of coordinates theoretically extends from 16 to 16384 units, such extremes are rarely encountered in typical font designs. Additionally, the command types undergo one-hot encoding, whereby each instruction is transformed into a vector of floating-point values, creating a standardised numerical representation suitable for neural network processing.

After the normalisation, the data are being transformed into a sequence of numerical values. Each sequence element consists of a command type identifier followed by coordinate pairs, creating a standardised format that preserves the path construction logic whilst being compatible with machine learning architectures.

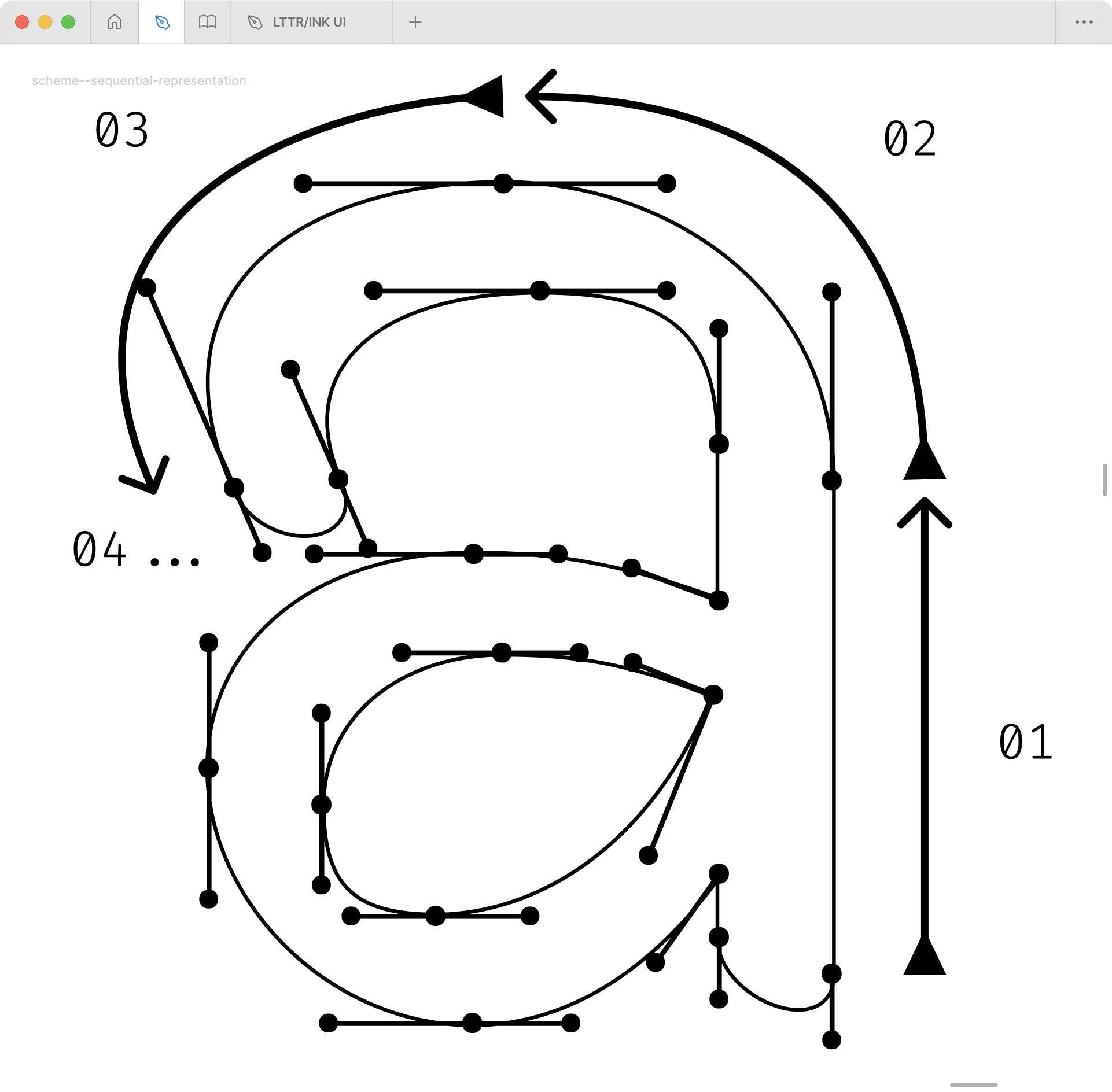
Native .glyphs representation:

nodes = (
    (38,0,l),      // line point
    (131,233,o),   // off-curve control point
    (225,467,o),   // off-curve control point
    (318,700,c),   // curve point
    (411,467,o),   // off-curve control point
    (505,233,o),   // off-curve control point
    (598,0,c)      // curve point
);

In one sequence, commands like l, o, and c can be represented with three positions (e.g. 1.0, 0.0, 0.0), while coordinates are represented with two positions (e.g. 0.037, 0.000). Then, the whole sequence length has five positions.

tensor([[1.0, 0.0, 0.0, 0.037, 0.000],
        [0.0, 1.0, 0.0, 0.128, 0.228],
        [0.0, 1.0, 0.0, 0.220, 0.456],
        [0.0, 0.0, 1.0, 0.311, 0.684],
        # ...
       ])

Native .otf representation:

38 0 moveto               % starting point
131 233 225 467 318 700   % control points and destination
curveto                   % curve command
411 467 505 233 598 0     % control points and destination
curveto                   % curve command

In one sequence, commands such as moveto and curveto can be represented with three positions (e.g. 1.0, 0.0, 0.0), whilst coordinates are represented with two positions (e.g. 0.037, 0.000). Thus, the whole sequence length maintains five positions.

tensor([[1.0, 0.0, 0.0, 0.037, 0.000],
        [0.0, 0.0, 1.0, 0.128, 0.228],
        [0.0, 0.0, 1.0, 0.220, 0.456],
        [0.0, 0.0, 1.0, 0.311, 0.684],
        # ...
       ])

The sequential nature of vector data representation exhibits notable similarities to natural language processing methodologies. Contemporary approaches leverage established architectures from language modelling, including recurrent neural networks (RNNs), variational autoencoders, and transformer models.