3.1.1. Font Blending

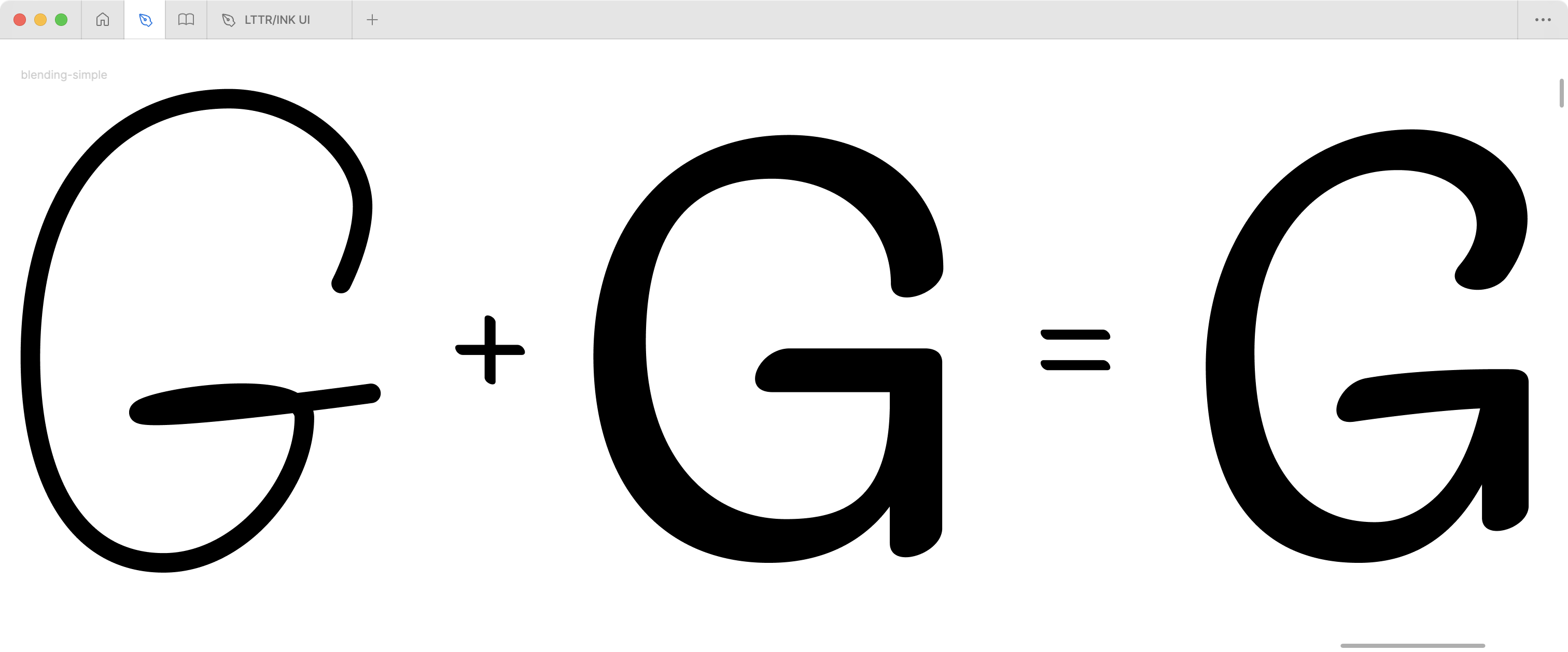
Figure illustrates the blending of two fonts. From the left, the first letter illustrates a casual handwritten style, and the second image illustrates a formal sans serif grotesque. The result illustrates the blending of both styles into a new style.

Every type designer who stumbled upon a variable font 1 project has faced a frequent issue. Some parameters of variable font masters 2 don’t match, which prevents the calculation of the required instances in the design space 3. Unlike variable font interpolation, the interpolation methods of machine learning models don’t necessarily face the issue and don’t even require masters to match all the properties.

Variable font interpolation In type design, the interpolation is used to populate intermediate font styles between two or multiple font style masters. Key components for interpolation are

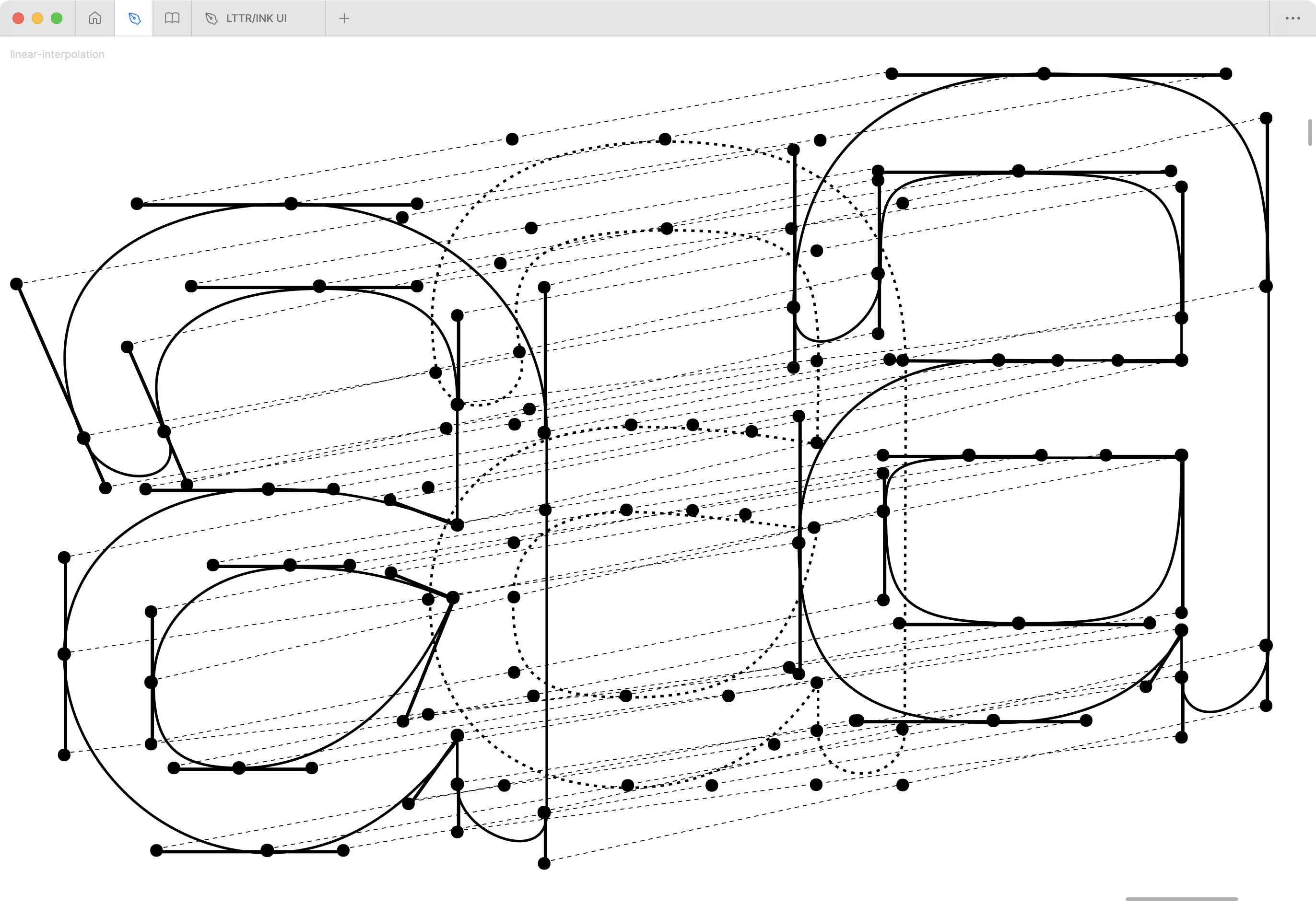
The interpolation process calculates intermediate positions Pi of glyph outlines control points P with coordinates (x, y) at a given value v along an axis. The linear interpolation formula commonly used in vector graphics is Pi​(v) = Pmin​ + v ⋅ (Pmax​ − Pmin​) 4 where:

Figure illustrates the principle of linear interpolation. On the left and right are masters, and in the middle is an interpolation instance.

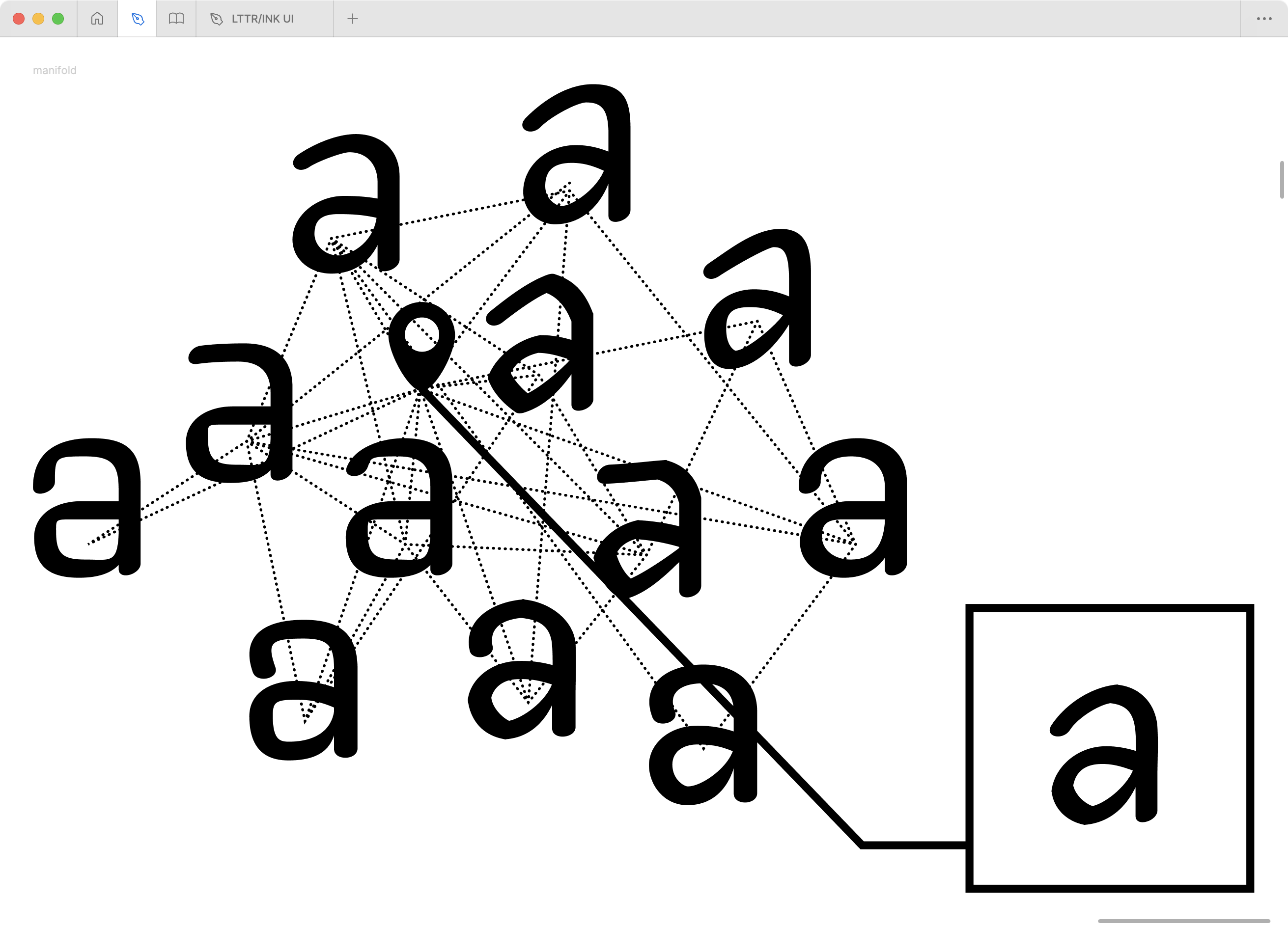
Traversing connected space This method is somewhat similar to traditional variable font interpolation and allows blending fonts by representing the whole library in a connected space called a manifold. Font-MF (Campbell and Kautz 2014) employs a Gaussian process latent variable model (GP-LVM) (Lawrence 2005) to represent a manifold (Goodfellow, Ian, Bengio, Yoshua, and Courville, Aaron 2016, 157) of 46 fonts from Google Fonts library (Google, n.d.). A manifold is already a connected space and can be presented as a map. The blending is performed by traversing through this map 5. Hence, blending is not performed between two fonts but within the learned representation. Akin to traversing within Alice’s dream, where shapes of the world transform fluently into another shape as moving through space – a spot of psychedelic experience in mathematics. The font-MF (Campbell and Kautz 2014; Neill Campbell, n.d.) method has the potential for type foundries to exploit their existing fonts as a tool to explore new ideas. The interface of the manifold map is arbitrary and can be replaced by commonly known sliders representing the axes of their fonts. The limitation of the Font-MF system lies in its representation. The original bezier curves are translated into a dense set of normalised polylines. The polylines will be scrutinised later in the representations survey.

Figure illustrates multidimensional manifold – a connected space of font shapes. The various letters represent their topological masters, the lines represent dimensional connections. Traversing through the connection in multidimensional directions causes changing the generated shape.

Font interpolation with machine learning models Unlike variable font interpolation, the machine learning model doesn’t calculate the position of control points between two font masters directly but leverages the representation of fonts in a so-called latent space. The objects within a latent space (in our case, the fonts) are encoded as multi-dimensional vectors that can be interpolated. 6. In other words, the latent space is like a mind that envisions what an interpolated shape between given fonts might look like.

Feature values might correspond to the pixels of an image, while in SVGs, the features are the frequencies of occurrence of SVG commands. The latent space font interpolation usually uses the same formula of linear interpolation Pi​(v) = Pmin​ + v ⋅ (Pmax​ − Pmin​) 7.

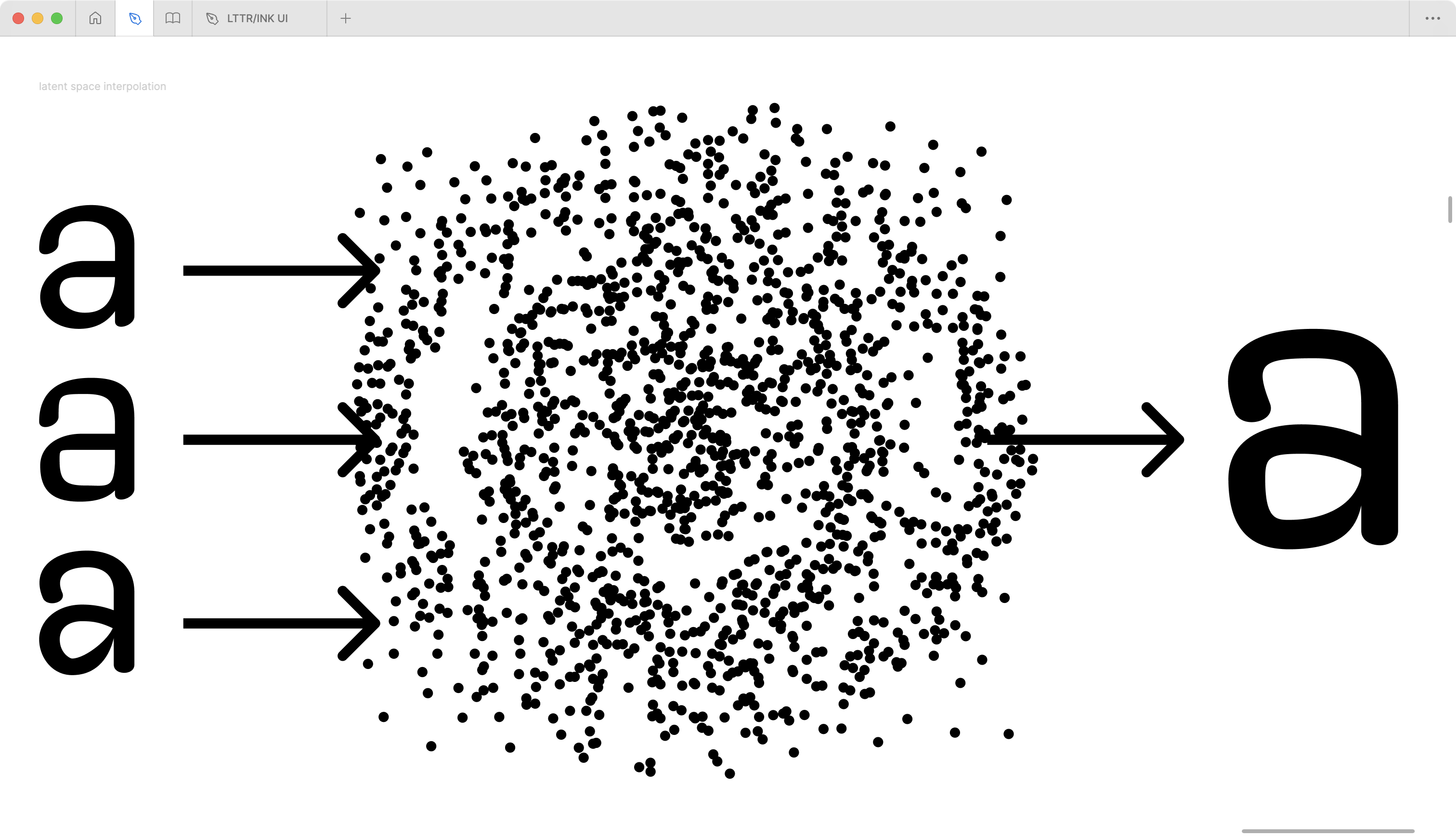
Figure illustrates latent space interpolation. On the left, there are fonts representing input fonts with distinctive style features. In the middle is a neural network with the learned representation of fonts – the latent space. On the right is the resulting font generated by the AI.

DeepSVG (Carlier et al. 2020) is the first to use deep learning-based methods for vector graphics. DeepSVG has brought latent space operations to interpolate between two vector graphics in order to provide vector animations between two SVG images. The system leverages the autoencoder (Goodfellow, Ian, Bengio, Yoshua, and Courville, Aaron 2016, 499) technique, which involves two components. First, the encoder works like a memory of the system that has a memorised representation of all the seen fonts. The encoder is tasked to give two latent vectors of the two given fonts that represent the recollection of the two fonts. The two vectors are linearly interpolated, and values are forwarded to the second network – decoder. In the end, the decoder generates a new font – the interpolated instance of the master fonts. Latent vectors f(a) and f(b) represent hierarchical SVG command structures. Since DeepSVG comes with a robust animation system, it can be used not only for the generation of ideas but also to visualise the ideas as animations between given fonts. Later, some descendants leverage latent space interpolation of sequences of SVG commands (Cao et al. 2023) or more sophisticated multi-modal representations that involve interpolation of multiple modalities (Yizhi Wang and Lian 2021; Yuqing Wang et al. 2023; Liu et al. 2023; Thamizharasan et al. 2023).

Campbell, Neill D. F., and Jan Kautz. 2014. “Learning a Manifold of Fonts.” ACM Transactions on Graphics 33 (4): 91:1–11. https://doi.org/10.1145/2601097.2601212.
Cao, Defu, Zhaowen Wang, Jose Echevarria, and Yan Liu. 2023. “SVGformer: Representation Learning for Continuous Vector Graphics Using Transformers.” In, 10093–102. https://openaccess.thecvf.com/content/CVPR2023/html/Cao_SVGformer_Representation_Learning_for_Continuous_Vector_Graphics_Using_Transformers_CVPR_2023_paper.html.
Carlier, Alexandre, Martin Danelljan, Alexandre Alahi, and Radu Timofte. 2020. “DeepSVG: A Hierarchical Generative Network for Vector Graphics Animation.” October 22, 2020. https://doi.org/10.48550/arXiv.2007.11301.
Goodfellow, Ian, Bengio, Yoshua, and Courville, Aaron. 2016. Deep Learning. MIT Press. https://www.deeplearningbook.org/.
Google. n.d. “Google Fonts.” Google Fonts. Accessed January 26, 2023. https://fonts.google.com/noto.
Lawrence, Neil D. 2005. “Probabilistic Non-linear Principal Component Analysis with Gaussian Process Latent Variable Models.” J. Mach. Learn. Res., December.
Liu, Ying-Tian, Zhifei Zhang, Yuan-Chen Guo, Matthew Fisher, Zhaowen Wang, and Song-Hai Zhang. 2023. “DualVector: Unsupervised Vector Font Synthesis with Dual-Part Representation.” May 17, 2023. http://arxiv.org/abs/2305.10462.
Neill Campbell. n.d. “FONT-MF Demonstration.” FONT-MF Demonstration. Accessed January 18, 2023. http://vecg.cs.ucl.ac.uk/Projects/projects_fonts/projects_fonts.html.
Thamizharasan, Vikas, Difan Liu, Shantanu Agarwal, Matthew Fisher, Michael Gharbi, Oliver Wang, Alec Jacobson, and Evangelos Kalogerakis. 2023. “VecFusion: Vector Font Generation with Diffusion.” December 16, 2023. http://arxiv.org/abs/2312.10540.
Wang, Yizhi, and Zhouhui Lian. 2021. “DeepVecFont: Synthesizing High-quality Vector Fonts via Dual-modality Learning.” October 13, 2021. https://doi.org/10.48550/arXiv.2110.06688.
Wang, Yuqing, Yizhi Wang, Longhui Yu, Yuesheng Zhu, and Zhouhui Lian. 2023. “DeepVecFont-v2: Exploiting Transformers to Synthesize Vector Fonts with Higher Quality.” March 25, 2023. https://doi.org/10.48550/arXiv.2303.14585.

  1. Variable fonts are an evolution of the OpenType font specification that enables many variations of a typeface to be incorporated into a single file rather than having a separate font file for every width, weight, or style.↩︎

  2. Variable font masters represent extreme design along one or more axes, e.g. lightest and heaviest on the weight axis↩︎

  3. Design space is a set of axes that represent a specific design variation, e.g. weight, width, or slant.↩︎

  4. There are various notations of linear interpolation formulas. In this text, two variants are presented: the variable font interpolation formula commonly used in vector graphics and the latent space interpolation formula widely used in a mathematical context. Both variants represent the same values: 1. interpolated value; 2. two extremes on an interpolated axis; 3. parameter ranging from 0 to 1]↩︎

  5. The Font-MF project website has an interactive demo allowing users to traverse through the manifold. URL: http://vecg.cs.ucl.ac.uk/Projects/projects_fonts/projects_fonts.html↩︎

  6. A multi-dimensional vector (in pattern recognition and machine learning) is a feature vector that consists of numerical features representing some object.↩︎

  7. There are various notations of linear interpolation formulas. In this text, two variants are presented: the variable font interpolation formula commonly used in vector graphics and the latent space interpolation formula widely used in a mathematical context. Both variants represent the same values: 1. interpolated value; 2. two extremes on an interpolated axis; 3. parameter ranging from 0 to 1]↩︎

License

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .

Creative Commons License

Citation

If this work is useful for your research, please cite it as:

@phdthesis{paldia2025generative,
  title={Research and development of generative neural networks for type design},
  author={Paldia, Filip},
  year={2025},
  school={Academy of Fine Arts and Design in Bratislava},
  address={Bratislava, Slovakia},
  type={Doctoral thesis},
  url={https://lttrface.com/doctoral-thesis/},
  note={Department of Visual Communication, Studio Typo}
}